二次方斜坡速度，其位置函数是三次方，二次方的速度用做曲线衔接比较方便，其加速度是一次，即直线加速度和直线减速度，运行时加速度无突变，如下图。
二次方曲线规划比较复杂，因其加加速度生效，加速度连续，速度连续，所以需要考虑速度饱和、位置饱和两种情况，非常复杂。例如因距离过短，需要限定速度运行，速度限定后可能会再限定加速度或者减速度，排列组合情况很多，本人未能全部解耦，只讲一种特殊情况，fAcc=fDec。

二次方因其加速度连续，适用于大负载运行，启停较为柔和。

假设距离、速度不被其余参数限定，按照下面曲线图来计算加减速时间的话，需要对曲线分为7段。
1加加速、2匀加速，3减加速，4匀速，5加减速，6匀减速，7减减速，下图在加加速度fJerk曲线中已标出。

简单讨论此种特殊情况。
加速时间分为3段，匀速时间1段，减速时间3段，其计算公式如下：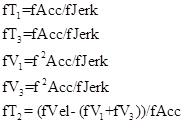




计算出时间和速度后，利用对称性可再计算出位置，利用梯形面积公式


此时需要fP1+fP3和fPos的大小，来决定是否存在4匀速段。
除4匀速段需要判断是否存在之外，还需要判断2匀加速，6匀减速是否存在，排列组合较多，此处不再过多阐述，程序中只讨论了fAcc=fDec的情况。